Glossary of Terminology
3D Metrology
3D scanning, also referred to as 3D digitizing, is the utilization of a three dimensional data acquisition device (3D scanner) to acquire a multitude of X,Y,Z coordinates on the surface of a physical object. In simplest terms, it is taking a physical object and creating a digital blue print.
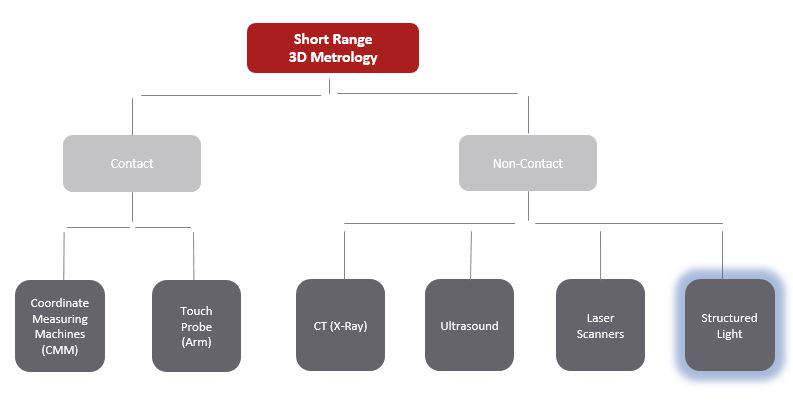 |
Structured Light 3D Scanners: Also known as white light 3D scanners, blue light 3D scanners, optical metrology, or full-field metrology, captures measurements based on the principles of triangulation utilizing a projector that shines a fringe pattern across the part’s surface and as the patterns rapidly shift during each scan, the camera(s) capture(s) the displacement to calculate the 3D coordinate measurements.
Initial Alignments
Prealignment: The prealignment aligns the actual data (measurements, meshes ...) automatically to the nominal data, independently of start positions. A prealignment can be carried out with a subsequent automatic best-fit alignment.
3-Point Alignment: The 3-Point Alignment is a manual prealignment method to roughly align actual data (measurements, meshes ...) to nominal data (CAD). This method is used if e.g. the automatic prealignment cannot function properly. The prealignment is made based on three points that are clicked with Ctrl and LMB (left mouse button) on the nominal data and three points with approximately the same position on actual data.
3-2-1 Alignment: The 3-2-1 alignment provides for transforming 3D objects according to the 3-2-1 rule by clicking on reference points or 3D points. The 3-2-1 alignment transforms your measuring and mesh data into a defined coordinate system.
Best-Fit by Reference Points: This alignment method can only be used for measurement series. For this method, the complete 3D coordinates of at least 3 arbitrary reference points need to be known and must be available in a file. The software automatically identifies these points in your measuring project if the imported coordinates describe a reference point constellation that can be found in the measuring project as well. The measurement series then is transformed into the coordinate system of these points.
Set As Aligned: After this function is used, the measuring project gets the status “aligned.”
Main Alignments
RPS Alignment: The RPS (Reference Point System) alignment is based on the fact that the RPS elements (points) on the nominal data create the actual elements on the actual data. During this process, the coordinate system of the actual data is aligned to the nominal coordinate system. For this process, you may adjust the effective direction of each link (XYZ). RPS alignment results in a defined and user-independent alignment. It is based on surface points or constructed elements that contain a point. This RPS alignment function minimizes deviations (square error) through all used RPS points. The simplest procedure to enter all necessary data for the RPS alignment in this menu is to import a measurement series. One other way is to construct the RPS points on the nominal data and to assign the measurement principle to the points.
RPS With Tolerances: The function RPS With Tolerances offers the possibility to limit not only the effective direction of the RPS element (point) but also its effective range. You may set the effective range manually or use the tolerance of the RPS element directly.
Local Best-Fit: The aligning method Local Best-Fit aligns the actual data to the nominal data via a best fitting of the selected surface in the 3D view.
Local Best-Fit with Tolerances: The aligning method Local Best-Fit with Tolerances aligns the actual data to the nominal data via best fitting, taking into account defined tolerance limits. It is a special alignment method, e.g. for assembly parts, in order to get information about the fitting-in of the components or for castings which need to be worked on in a further milling process (check if there is enough material for milling).
Plane-Line-Point Alignment: The alignment method Plane-Line-Point aligns actual data via constructional elements plane, line and point to the nominal data. Create the elements line, point, and plane on the nominal and actual data on suitable areas according to the 3-2-1 rule. For more information about 3-2-1 rule see 3-2-1 Alignment. If you assign a measuring principle to the nominal elements plane, line and point, the actual elements can be created automatically. The nominal and actual data has to be pre-aligned, see Prealignment. If you construct the nominal and actual elements separately from each other, no Prealignment is necessary.
Measuring Principle
A measuring principle is a method of creating actual elements based on nominal elements (CAD data). In addition, the created actual element is always linked to the nominal elements.
Actual section: This measuring principle creates an actual section on the actual mesh based on a nominal section.
Adapter: This measuring principle can be used for edge points, spheres, and cylinders. A nominal edge point or a nominal geometry (sphere or cylinder) creates corresponding adapters elements on the actual data. If measuring data contains a real and identified adapter within a max distance of 20mm (adjustable) from the nominal element, it is displayed in green in the 3D view.
Fitting Element: This measuring principle can be applied to points, lines, planes, circles, slotted holes, rectangles, cylinders, cones, and spheres. A nominal geometry is created based on corresponding point selections on the actual data.
Gray Value Feature: (Sheet Metal) Respective 3D points are created with the help of contrast lines (gray values) in the 2D images. The function calculates the gray value feature points by extending the surrounding area of the contrast line and taking into account the respective 3D points
Intersection with mesh: A vector point on the nominal data creates via Intersection with mesh in the direction of the normal intersection with the actual data.
Intersection with mesh relative: For sheet metal parts ex. have a spring in comparison to their CAD data, it may be necessary to measure a point relative to another nominal point. By means of a relative measurement you may determine ex. the actual deviation of a point after the measured part has been mounted and the spring is gone.
Intersection with curve, Section: An edge point on the Nominal data creates an intersection point with actual curves, actual edges or actual sections using this measuring principle.
Line and circle of curvature: This measuring principle is useful for inspecting car body lines. It follows in selected are curvatures and, in this selected area, creates an actual line of curvature which runs through the determined vertices of the curvatures. Based on this actual line of curvature, the curvature radius can be analyzed in a second step perpendicular to the line or curvature taking into account the neighboring area.
Link to actual Element: You may directly assign an actual element to a nominal element.
Online Adapter: This measuring principle can be use or edge points, spheres and cylinders. A nominal edge point or a nominal geometry (sphere or cylinder) creates corresponding adapters elements on the actual data which now can be measured “online."
Projected offset section: This measuring principle is suitable e.g. for the center point determination of pierced holes. Automatically creates auxiliary elements in the actual data (ex. plane, section, fitting circle) and computes the results by means of projection methods.
Project onto mesh: A point on the nominal data creates a point on the actual data within the shortest distance.
Reference Construction: Means that elements on the actual data are created in the same way as on the nominal data.
Surface Point: with this function you may create, besides the simple deviation labels, complex labels based on a surface comparison. (Prerequisites: have a surface comparison to CAD created).
Touch Cylinder: A defined nominal cylinder touches an actual mesh in a defined direction and creates an identical actual cylinder at the position resulting either from the first contact point with the actual mesh or from two contact points with the actual mesh, depending on the settings you define.
Touch Circle: A defined nominal circle touches an actual mesh in a defined direction and creates an identical actual circle at the position resulting either from the first contact point with the actual mesh or from two contact points with the actual mesh, depending on the settings you define.
Touch Point Disc: A vector point on the nominal data (ex. a surface point) creates a touch point on the actual data in the vector direction of the nominal point. The touch point results by touching the actual data with a defined circular disc.
Touch Point Edge: A nominal point with two direction vectors (ex. an edge point) creates a touch point on the actual data in the direction of the trimming vector of the nominal point. The touch point results by touching the actual data with a defined edge.
Touch Point Edge with Direction: A nominal point with a normal vector (ex. surface point or edge point) creates a touch point on the actual data in the direction of the normal vector of the nominal point. The touch point results by touching the actual data with a defined edge.
Touch Probe: This measuring principle can be used for many construction elements (points, bodies, holes, distances ...) ex. A nominal surface point that was assigned the measuring principle touch probe creates an actual point which at first is not computed in order to compute this point you need to touch this point manually on the measuring object using a calibrated touch probe and start a measurement.
Industry Terms and Acronyms
Accuracy:The closeness of a measured object to what CAD says it should be.
AM: Additive Manufacturing.
API: Application Programming Interface.
AEC: Architecture, Engineering and Construction (industry)
BIM: Building Information Modeling.
CAD: Computer-Aided Design.
Calibration: Comparison of measurement values delivered by a device under test with those of a calibration standard of known accuracy.
CNC: Computer Numerical Controlled.
CMM(Coordinate-measuring machine): A device that measures the geometry of physical objects by sensing discrete points on the surface of the object with a probe.
Dimensional Metrology: The science of calibrating and using physical measurement equipment to quantify the physical size of or distance from any given object.
Full-Field Inspection: Full-field inspection is the creation of thousands, sometimes millions of high-accuracy data points covering the entire surface of the part. We then overlay the scan data to the CAD model (the perfect part) and compare the nominal specifications to the actual data.
Gage R&R (Gage Repeatability and Reproducibility): A methodology used to define the amount of variation in the measurement data due to the measurement system. It then compares measurement variation to the total variability observed, consequently defining the capability of the measurement system. Measurement variation consists of two important factors, repeatability, and reproducibility. Repeatability is due to equipment variation and reproducibility is due to an inspector or operator variation.
IIoT: Industrial IoT
MBD: Model-based definition (also "digital product definition" or "product information modeling"). Model-based definition is the practice of using 3D models within 3D CAD software to define individual components and product assemblies.
Micron or Micrometer (µm): A metric unit of measure for a length equal to 0.001 mm, or about 0.000039 inches.
MES: Manufacturing Execution Systems
MRO: Maintenance Repair and Operation
NNS: Near Net Shape
Parametric Model: ACAD model that can be edited and changes will propagate through the model automatically preserving the relationships between features.
Photogrammetry:Non-contact imagery that takes 3D coordinate measurements (XYZ) through photographs.
PMI: Product and manufacturing information, also abbreviated PMI, conveys non-geometric attributes in 3D computer-aided design and Collaborative Product Development systems necessary for manufacturing product components and assemblies.
POC: Proof of Concept
Polygonal Modeling: An approach for modeling objects by representing or approximating their surfaces using polygon meshes .
Reverse Engineering:is the process by which a man-made object is deconstructed to reveal its designs, architecture, code or to extract knowledge from the object.
.stl file: A point cloud file comprised of scanning data used for inspection and analysis software
Validation:Demonstration by test or analysis that an instrument, system, or procedure is fit for a certain task.
Verification:The proof, by means of objective evidence, that an item meets its specification requirements. In dimensional inspection the object’s dimensions would be measured and compared to the drawing or CAD model of the object.







